玖月网络

如何求正态分布的分布函数？这是标准的正态分布密度函数(如图):如果是计算概率，就要用到分布函数，但它的分布函数不能写成正态解析表达式。这是标准的正态分布密度函数(如图):如果是计算概率，就要用到分布函数，但它的分布函数不能写成正态解析表达式，正态分布的概率密度函数？对于非标准正态分布，可以通过标准化(将给定的分布转化为标准正态分布)，然后使用标准正态分布函数来计算。

这是标准的正态分布密度函数(如图):如果是计算概率，就要用到分布函数，但它的分布函数不能写成正态解析式。一般的计算方法是计算标准正态分布函数在各点的分布函数值并制成表格，在实际计算中查表求概率。非标准正态分布函数可以转换成标准正态分布再计算。当μ维随机向量具有相似的概率规律时，称这个随机向量服从多维正态分布。

标准正态分布函数也叫CumulativeDistributionFunction(简称CDF)或Phi函数，用φ (x)表示。是指随机变量的概率密度函数在服从标准正态分布(均值为0，标准差为1)时，位于负无穷大和给定值X之间的累积概率。标准正态分布函数的数学表达式为:φ (x) (1/√ (2π)) ∫横轴区间内的面积(μ σ，μ σ)为68。%，横轴区间(μ 1.96σ，μ1.96σ)内的面积为95。%，横轴区间内的面积(μ2.58σ) X~N(μ，σ):一般正态分布:均值为μ，方差为σ；P(μσ).正态分布的概念正态分布是一种概率分布。

第一个参数μ是一个服从正态分布的随机变量的均值，第二个参数σ 2是这个随机变量的方差，所以正态分布记为N(μ，σ 2)。服从正态分布的随机变量的概率规律是，取μ附近的值的概率大，取离μ较远的值的概率小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正态分布的密度函数的特征是:关于μ对称性，在μ处达到最大值，在正(负)无穷处取值为0，在μ σ处有拐点。

这是标准的正态分布密度函数(如图):如果是计算概率，就要用到分布函数，但它的分布函数不能写成正态解析式。一般的计算方法是计算标准正态分布函数在各点的分布函数值并制成表格，在实际计算中查表求概率。非标准正态分布函数可以转换成标准正态分布再计算。正常曲线呈钟形，两端低中间高，左右对称，所以人们常称之为钟形曲线。

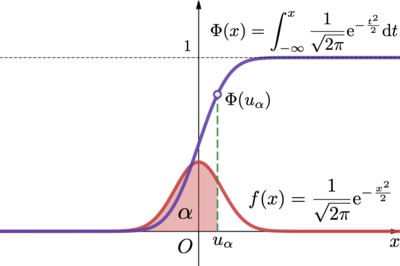
标准正态分布的密度函数:f (x) (1/√ 2π) exp (x 2/2)。Exp (x 2/2)是e的x 2/2的幂，它的定义域是(∞，∞)。从概率密度的表达式中可以看出，f(x)是一个偶函数，即f(x)的像关于y是对称的，φ (x)定义为服从标准正态分布的随机变量X的分布函数，其值是f(x)关于X的积分，从∞乘积到X，从f(x)像中，φ(X)的值相当于f(x)曲线下X轴上(∞，X)的面积

正态分布的概率密度函数特征的集中性:正态曲线的峰值位于正中心，也就是均值所在的位置。对称性:正态曲线以均值为中心，左右对称，曲线两端从不与横轴相交。均匀变异:正态曲线从均值所在的地方开始，分别向左右两侧逐渐均匀递减。曲线与横轴之间的面积始终等于1，等价于概率密度函数的函数从正无穷到负无穷的概率为1。即频率之和为100%。

standardnormaldistribution(英文、德文)是数学、物理、工程等领域中非常重要的概率分布，在统计学的许多方面都有很大的影响。期望值μ0，即曲线图像对称轴为Y轴，标准差σ1条件下的正态分布，记为n (0，1)。因为x ~ n (μ，σ 2)，

不，域是不对称的。不是这样的。即使是对称域的标准正态分布也不会是偶函数。F (x) (1/√ 2π) * E (x 2/2)是一个偶函数但只是它的密度函数而不是它的分布函数。分布函数就是这个密度函数的积分，积分结果不是初等函数。所以根据偶函数的定义，F(x)表示密度函数在x左侧的积分面积，F(x)表示密度函数在x左侧的积分面积。

标准正态分布函数的公式如下所示:1。密度函数关于平均值对称；2.平均值与其统计模型和中间值相同，3.68.函数曲线下面积的%在平均值的标准偏差范围内。4.95.%的面积在平均值的两个标准偏差范围内，5.99.%的面积在平均值周围三个标准差的范围内。

正态分布 表达式